Batch 2 - Class 99 - Graphene Trampolines
Pre-Class Problem:
- Can you move as few cards as possible so that the total in the two columns becomes equal

- Answer: Swap 9 and 8, and turn 9 upside down!
Attendance: Anisha, Smiti, Tishyaa, Liza, Khushi, Arnav, Anishka, Anshi
Class Notes:
Richard Smalley (1943-2005) was awarded the Nobel Prize in Chemistry for discovering that he could make tiny soccer balls out of carbon atoms. In 2005, he started to shrink, and became so small that he could bounce on tiny trampolines that make up graphene. Richard Smalley spent his time making graphene trampoline puzzles.
Here is one. Smalley can move on the trampoline basis roll of dice. He can not go back to a cell he has already visited.
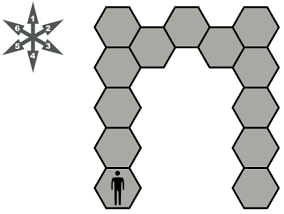
- What turn of dice does he need to roll to start moving?
- What turn does he need for the next roll?
- Can you trace his path as he starts to roll successively?
- Instructor Notes: At the top fork, consider both cases to illustrate that in one case the game stops without covering all cells. In the other one can move on.
- This trampoline has both success and failure possible, hence we will color it yellow.
Lets try another trampoline. We will try a few different starting points, and then color a cell yellow, green or red basis whether starting out from that cell can lead to both success and failure, only success or only failure. Try this one out and color all cells basis success and failure possible there.
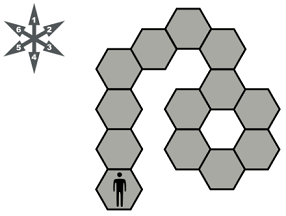
- Can you figure out the probability of success from each yellow cell?
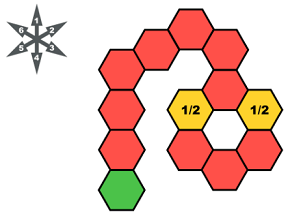
- Can you figure out the probability of success on the original trampoline?
- Answer: 1/4
Solve for a few more. Older students, find the probability of success for the yellow cells.
- Homework Challenge: Can you solve for this one?
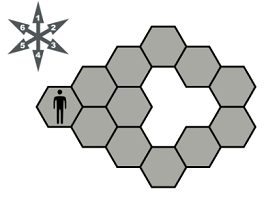
- Answer: 29/36
Card Magic!
Note that this trick does not work all the time. It works about 85% of the time.
Trick: The victim chooses a number (say between 1 and 10), and then you start at the beginning of a shuffled deck (or better, a shuffled pair of decks) and you deal the cards face up, slowly, one at a time. As you deal, the victim silently counts the cards until his number of cards is dealt. In other words, if he chose 5, he will silently count the cards you deal as 1, 2, 3, 4, 5. When his card (the fifth in this example) is reached, he looks at the rank of that card which will be from ace (= 1) to king. If the card is a face card (jack, queen or king), count its rank as 5 (This is not what we did in class). As soon as he sees that card, the rank is his new number, and he begins counting from one again beginning with the next card you turn up. Repeat this process, and each time he reaches his count, that card’s rank is his new number. Finally, as he is counting up the deck will run out, and he will not have gotten to his number. Whatever card he was using as his latest number is his final card. At this point, you tell him what that card is.
Discussion: The reason this works is that as you’re both going through the deck, if you ever happen to hit the same card as the victim, from then on you will both be locked into the same “path” through the rest of the deck and will certainly arrive at the same final card. You can make a mathematical estimate as follows. The “average” advance will be by: (1 + 2 + 3 + · · · + 9 + 10 + 5 + 5 + 5)/13 = 5.38 cards, so you will take, on average, about 52/5.38, or about 8 steps. The density of the victim’s cards is about 1/5.38 = .186, so there’s a 1 − .186 = .814 chance of a miss. But you have to miss all 8 times, and this will occur about (.814)8 = .174 so you’ll win about .836 of the time.
- What do you expect to happen if you are playing with two decks of card?
- What do you expect to happen if face cards are assigned face values (11 for Jack, 12 for Queen, 13 for King)?
- What do you expect to happen if cards are assigned value basis letters in their name (3 for ACE for example)?
This has mathematical application in cryptology to solve for discrete logarithms. Its called Pollard's Kangaroo method!
Homework
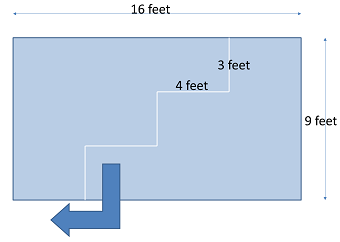
- (Geoffrey - 64) Mr Houseman wishes to lay down carpet on the floor of his kitchen, which is exactly 12 feet x 12 feet. He has a piece of carpet 16 feet x 9 feet, which is just enough to cover the area. However, he doesn't want to cut it in any more pieces that absolutely required. What is the minimum number of pieces he needs to cut the carpet to fit it back on the kitchen floor?
- Answer: 2 pieces
References:
Mathematical Puzzles, Geoffrey Mott-Smith